Cuando se realiza un estudio estadístico sobre una variable (por ejemplo, altura de los niños de una clase, equipo de fútbol preferido por los alumnos de un colegio, etc.) se comienza por obtener información (se mide a los niños, se les pregunta, etc.).
Dato estadistico es cada una de las informaciones que se obtiene (por ejemplo, Pedro mide 1,65 cm; Julián es aficionado del Barcelona, etc).
Vemos que el dato estadístico puede ser Numerico (por ejemplo, estatura) o cualitativo (por ejemplo, equipo de fútbol preferido).
Los datos obtenidos en la observación hay que ordenarlos y recogerlos en una tabla que se denomina tabla estadistica
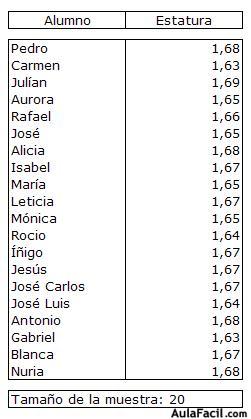
El número de observaciones realizadas se denomina tamaño de la muestra.
La frecuencia absoluta de un dato es el número de veces que se da un resultado concreto y la frecuencia relativa es el porcentaje que representa la frecuencia absoluta respecto del total.
La media aritmética representa el valor medio que toman los datos de una observación estadística. Se calcula sumando todos los resultados y dividiendo la suma entre el número de registros. La media aritmética tan sólo se puede calcular con datos numéricos (no se puede calcular con datos cualitativos).
Moda: es el resultado más repetido en una observación estadística (se puede calcular con datos numéricos y cualitativos).
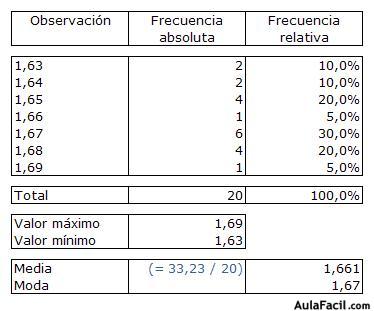
La media la hemos calculado sumando las 20 estaturas (33,23 cm) y dividiéndolo entre el número de datos (20).
Las frecuencias absolutas o relativas se pueden representar sobre una gráfica de barras en la que la altura de cada barra representa el valor de la frecuencia.
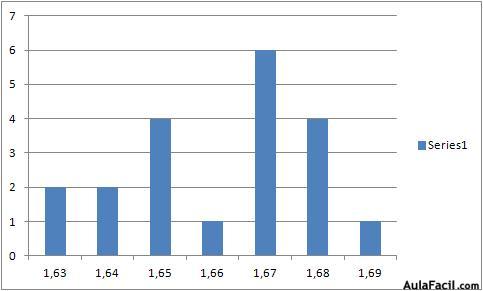
En este gráfico hemos representado la frecuencia absoluta.
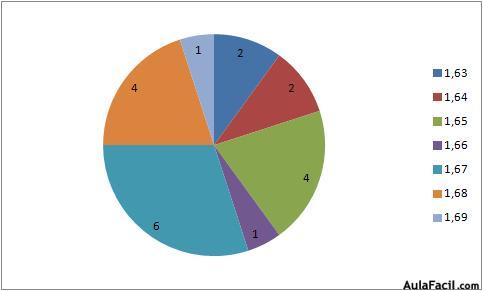
También se puede utilizar el diagrama de sectores para representar las frecuencias (absolutas o relativas). Se utiliza un círculo dividido en sectores; cada sector representa cada uno de los posibles valores que toma la variable que se mide; la superficie del sector mide el valor de la frecuencia (absoluta o relativa).
Histograma
, un histograma es una representación grafica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados, ya sea en forma diferencial o acumulada. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o la muestra, respecto a una característica, cuantitativa y continua, de la misma y que es de interés para el observador.
EJEMPLO
1. Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.
Construir la tabla de frecuencias.
| xi | fi | Fi | ni | Ni |
|---|---|---|---|---|
| 27 | 1 | 1 | 0.032 | 0.032 |
| 28 | 2 | 3 | 0.065 | 0.097 |
| 29 | 6 | 9 | 0.194 | 0.290 |
| 30 | 7 | 16 | 0.226 | 0.516 |
| 31 | 8 | 24 | 0.258 | 0.774 |
| 32 | 3 | 27 | 0.097 | 0.871 |
| 33 | 3 | 30 | 0.097 | 0.968 |
| 34 | 1 | 31 | 0.032 | 1 |
| 31 | 1 |

No hay comentarios:
Publicar un comentario